 |
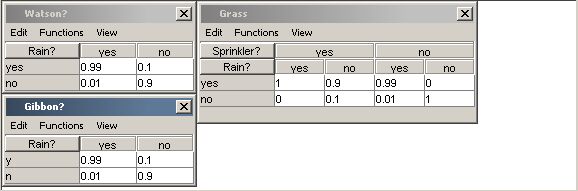
| 図 1: 枠モードで表示された表 |
Hugin グラフィカル・ユーザー・インタフェースは,サイズ変更,選択された列を閉じる,グラフ表示モードなどを含むノード表の表示のためのパワフルな機能を数々提供します.さらに,ユーザーは2種類の表の構成方法を選択できます:
 |
| 図 1: 枠モードで表示された表 |
 |
| 図 2: タブ・モードで表示された表 |
枠モードは,複数の表が一度に表示できる利点があり,一方,タブ・モードは(複数の表が開かれても)とてもコンパクトであり,表のナビゲートがより簡単です.用意された表モードは,プリファレンスで設定でき, 表の表示メニュー中の"表モードをトグル" 項目を選択して変更できます.
離散確率ノードの確率と効用ノードの効用は,それぞれ,手動(すなわち,クリック・アンド・タイプ操作で直接)で指定でき,あるいは強力な数式の指定によって間接的に指定でき,それは(適切な場合)作業を大幅に短縮します.
4種類の表について,編集メニュー, 関数メニュー, 表示メニューを含むメニューバーがあります.
編集モードで表パネルを開いて作業中の場合, 現在選択されているノードは,表パネル中に表示されたそれらの表を持ちます.
離散確率ノードと効用ノードでは, ノードは2つのモードがあります:
 |
|
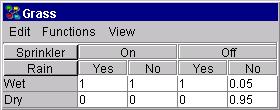
図 1: 手動モードでのCPT. |
 |
|
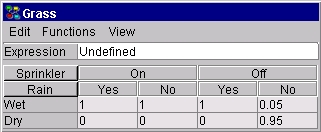
図 2: 数式モードでのCPT. |
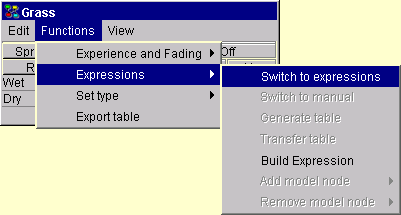
2つのモードの間で切り替えるには,ノード表の関数メニューで適切な項目を選びます.図3参照.
 |
|
図 3: 数式モードの選択. |
数式モードでは, 数式が手動または 数式ビルダーのどちらかで指定できる1つまたは複数の編集可能なテキスト・フィールドがあります.モデル・ノードのステートの数により多数のテキスト・フィールドが利用可能です.モデル・ノードが指定された場合,テキスト・フィールドは1つだけあります(すなわち,すべての親コンフィギュレーションで同じ数式が使用されます).
離散確率ノードでは,この関数は,ノードの親(これも離散確率ノード)のステートの各コンフィギュレーションでの,ノードのステート上の条件付き確率分布を表します. 条件付き確率分布(または,親がない場合は周辺確率分布)は,条件付き確率表(CPTと略す)として表現されます.図 4 は, 親 Rain とSprinkler を持つノードGrass のCPTの事例を示します.
|
|
|
図 4: 親 Rain と Sprinkler を持つノード GrassのCPT. |
離散確率親 I と連続親 Z を持つ連続確率ノードでは, 関数は,親の値に条件付けられる(1次元の)ガウス型分布を表します:
![]()
[これはCG 分布として知られます.] 平均値は連続親に線形的に従属し,分散は連続親には従属しないことに注意してください.しかしながら,その線形関数と分散は,離散親に従属することが可能です.(これらの制約は,正確な推論が可能であることを保証します.)したがって,離散親の各コンフィギュレーションについて,平均と分散パラメータが指定されなければ ならず,また各コンフィグレーション親の回帰パラメータも指定されなければなりません.図 5 は,離散親 Burning Regimen (Burn) および Waste (Waste Type),および連続親 Filter Efficiency (Efficiency)を持つ連続ノード Dust Emission (Emission)の表を示します.
|
|
|
図 5: 親 Burn と Wasteを持つ連続ノードEmissionの表. |
各効用ノードでは,関数は効用関数を表すノードに関連づけられています.ここで,効用値は,離散確率ノードおよび決定ノードであり得る親の各コンフィギュレーションについて指定されなけければなりません.図 6 は,離散確率ノード Oilと離散決定ノード Drillを親として持つ効用ノード Utility の表を示します.
|
|
|
図 6: 親 Drill と Oil を持つ効用ノードUtilityの表 . |
各決定ノード は,決定表に関連づけられています.これは,決定ノードに関連づけられたさまざまな決定オプションの単一の列を含むだけなので,とても単純です.図 7 は,決定オプション "Buy now", "Wait", "Don't buy"を持つ決定ノードDの表を示します.
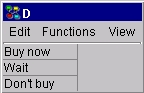 |
| 図 7: 決定ノード D の決定表. |
編集メニューは,下記の機能を提供します(図8参照):
コピーおよび貼り付け操作はアプリケーション間でも動作することに留意してください(たとえば,Hugin のノード表から Excel, Word, Emacsなど,またはその逆).
|
|
|
図 8: ノード表の編集メニュー. |
関数メニューは,下記の機能を提供します(図9参照):
|
|
|
図 9: ノード表の関数メニュー. |
|
|
|
図 10: 作成されて表示された経験表と減退表. |
表示メニューは,下記の機能を提供します(図11参照):
|
|
|
図 11: ノード表の表示メニュー. |
- 数字のみを利用するノーマル・モード.
- 数字に対応する長さのバーを数字に重ね表示するバー・モード(図16参照).
- バーのみが表示される純粋バー・モード(図17参照).
- 自動正規化 は,バーをドッグしたときに,数字(バーの長さで表現される)の合計が1になるように,その分布に属する他のバーが自動的に調整される.
表示モードの詳細については,次の節 を参照.
表パネルが開いていると, ネットワーク・パネルで選択されたノードの表が表示されます .Hugin グラフィカル・ユーザー・インタフェースは,ノード表を表示するためのパワフルな機能を持ちます:
ノード表の枠(すなわち,表を表示する内部ウィンドウ)は,枠の境界でマウスの左ボタンをクリックしてホールド(すなわち,ドラッグ)することにより,任意にサイズ変更できます.表のセルの幅は対応してサイズ変更されます.第1列(親とステート名を格納)の幅は,第1列と第2列の間の境界で,左マウス・ボタンをドラッグしてサイズ変更できます.親やステートの名前がとても長かったり短かったりする場合に,これが便利です.
ノード表での親の出現順序は,ノードのプロパティ・パネルの表タブ で変更できます.これは,分布の集合とグルーピングするのに便利です.
また,選択された分布の集合のより良い表示のために,親ステートの適切なラベルをダブル・クリックして,列(親コンフィギュレーションに対応)の集合 を閉じることができます.図 12 は,親 C1, C2, C3, C4を持つノードC5 の表(の一部)を示します.ここで,ステート "State 2"でのC1の確率分布で作業することに興味があるとします.1つの選択肢は水平のスクロール・バーを使用することでしょう.もう1つ,とても簡単でより便利なアプローチは,C1 が ステート"State 1"にあるところの表の部分を閉じることでしょう.これは, C1 行の"State 1"とラベルづけされたテキスト・フィールドをダブル・クリックすることで実現します.
|
|
|
図 12: 親ノード C1 のステートが "State 2"である列が閉じられた状態のノードC5 の表. |
図 13 は,結果の表を示します.小数点以下のすべての桁が見えるようにセルの幅が変更されていることに注意してください. 一般的に,親のステート・セクション中のセルは,最後以外のすべての親の行に対してダブル・クリックされることができ,対応する列が閉じられます.図 14 は, C4 が "State 1"である以外のすべての親ノードのステートが閉じられた表を示します.
|
|
|
図 13: 親ノード C1 のステートが "State 1"であるすべての列が閉じられたノードC5の表. |
|
|
|
図 14: 親ノード C1, C2, C3 のステートが "State 1"であるすべての列が閉じられたノードC5 の表 |
閉じられた列は,その列の最上部のセルをダブル・クリックして開くことができます.
親の出現順序を変更すると(上記),あらゆる閉じられた列が開かれることに注意してください.
ときどき,数値的ではなくグラフィカルに確率分布を表示したり,指定したりするのが望ましいことがあります.Hugin グラフィカル・ユーザー・インタフェースは,3つの表示モードを選択することを可能にします: 数値のモード(ノーマル・モードと表記),数値と画像のモード(バー・モードと表記),画像のモード(純粋バー・モードと表記).お好みのモードを表示メニューの下で選択できます.図15参照.
|
|
|
図 15: 離散確率ノードの表の確率は,数値,画像または数値と画像の療法で表示できる. |
図 16 と図17 は,図 14 の表が,それぞれバー・モードと純粋バー・モードで表示されているところを示します.
|
|
|
図 16: バー・モードで表示されたノード C5 のCPT. |
|
|
|
図 17: 純粋バー・モードで表示されたノード C5 のCPT. |
確率のグラフィカルな指定は,バーを左マウス・ボタンでドラッグすることで実行されます.バー・モードまたは純粋バー・モードが選択されている場合,確率が変更されると,分布は自動正規化に設定されます.この機能は,表示メニューのサブ・メニューの表示モードの下で選択できます.
グラフィカルな表示と指定のモードは,離散確率ノードの中だけで利用可能なことに注意してください.
翻訳者:多田くにひろ(マインドウェア総研)