 |
|
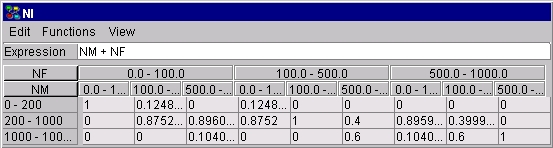
図 1: 数式から指定されたCPT.このCPTは,親 NM と NFを持つ離散確率ノード NI について指定されている. |
このチュートリアルは,離散確率ノードの条件付き確率表(CPT)と効用ノードの効用表の指定を簡単にするために,テーブル・ジェネレータ機能をどのように使用するかを説明する.このチュートリアルは,モデルと数式を用いて,これらの表がどのようにコンパクトに記述できるかを説明する.これはとくにある変数の条件付き確率分布が(少なくとも近似的に)特定の関数または分布の形に従う場合に有用である.このようなケースでは, 条件付き確率表(CPT)を手動で指定するのは,面倒なものである.
利用可能な数式の種類はノードの種類によるので,Hugin Decision Engineでサポートされているさまざまなノードのサブ・タイプを議論することで明らかになるであろう.
モデルは,離散ノードの一覧と数式の集合(ノードのステートの各コンフィギュレーションごとに1モデル)からなる.モデルのノードの一覧は,モデル・ノードと呼ばれる.
数式は,標準の統計的分布(たとえば,正規,二項,ベータ,ガンマなど),算術演算,標準の数学的関数(たとえば,対数,指数,三角,双曲線関数),論理演算(たとえば,andやif-the-else),関係(たとえば,<や=)を用いて構築される.
数式は,手動で構築する (数式のシンタックスを参照)こともできるし,一連のダイアログ・ボックスを用いて構築をガイドする 数式ビルダーの支援によって構築することもできる.
数式の中で用いられるさまざまな演算は,さまざまな戻り型とさまざまな引数の要件を持つ.したがって,数式を指定するための表現豊かな言語を提供するために,離散確率ノードと決定ノードを異なるグループに分類するのが都合よい(ノードのタイプの節も参照):
数字つきノードと区間ノードは,併せて数値ノード と呼ぶ.
とても頻繁に,1つまたは複数の親ノードのステートによって,異なる数式が必要なことがある.何段もネスト化されたif-then-else 式の使用は,これに対処する1つの方法である.しかしながら,結果の式は, しばしばとても複雑になり,ゆえに,目視検査で計算するのが難しく,したがって,保守が難しい.
複雑な数式を簡単にするために,モデル・ノードの考え方は,とても有用である.
上記で述べたように,CPTのモデルは,モデル・ノードの一覧とモデル・ノードのステートの各コンフィグレーションごとの数式からなる.つまり,モデル・ノードがない場合,モデルは単一の数式を格納する.
特定のモデルのモデル・ノードは,モデルが属しているノードの親の部分集合を構成する.この部分集合は,ノードのプロパティ・ダイアログ・ボックスの表タブの下で指定される.
モデル・ノードの使用の事例は,下記の事例 確率変数の離散化で説明する.
いくつかのアプリケーションで,男性と女性の数で確率分布を持つとしよう.ここで,分布は,区間 [0 - 100), [100 - 500), [500 - 1000)で定義される.そして, 我々は,2つの前者の分布を仮定して,人の合計数での分布を計算したいとしよう.これは簡単であるが, P(NI | NM, NF)を定義するのは面倒である.ここで, NI, NM, NF は,それぞれ,人の数,男性の数,女性の数の略である.この条件付き確率を指定するより都合のよい方法は, NM と NF がステート [0 - 100), [100 - 500), [500 - 1000)を持つ区間ノードで表現され, NI がステート [0 - 200), [200 - 1000), [1000 - 2000)を持つ区間ノードで表現され,そして,簡単な数式NI = NM + NFで P(NI | NM, NF) を表現するようにすることだろう.
その式を指定するために,まず,数式モードを選択する. ノード表のチュートリアルを参照.次に,左クリックで数式テキスト・フィールドを有効にする. 最後に,キーボードを使って,文字列 "NM + NF"(引用文字はなし)をタイプする.図1 は,この数式によるノードNIの結果の表と結果のCPTである.ここで,表示される数字は, "関数"メニューの"式"サブ・メニューから"表として表示"項目を選択して,数式から生成される.
 |
|
図 1: 数式から指定されたCPT.このCPTは,親 NM と NFを持つ離散確率ノード NI について指定されている. |
もう1つの事例として,公正な目とイカサマの目で, n 回サイコロを振ってn回6の目を得る確率を計算する問題を考えよう.公正な目でn 回サイコロを振って得られる6の目の数を意味する確率変数 X は,パラメータ (n, 1/6)を持つ二項分布に従う.したがって, 公正な目でn回サイコロを振って,k 回6の目を得る確率は,P(X = k)である.ここで, P は Binomial(n, 1/6)である.イカサマの目の場合,1回サイコロを振って6の目を得る確率が1/5であるとしたら,イカサマの目でn回サイコロを振って k 回6の目を得る確率は,'Q(X = k)である.ここで,Q は Binomial(n, 1/5)である.
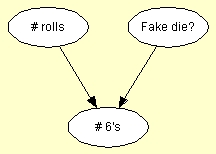
この問題のベイジアンネットワークを図2に示す.ここでノード n6s ( "# 6's"とラベルづけ)は,ノード n_rolls("# rolls"とラベルづけ)で表現するサイコロを振る回数に従属し,そして,ノード fake_die("Fake die?"とラベルづけ)で表現される目がいイカサマである確率に従属する.ここで,我々は n_rolls をステート 1, 2, 3, 4, 5を持つ数字つきノードとし,fake_die を論理ノードとし,そして, n6s をステート 0, 1, 2, 3, 4, 5を持つ数字つきノードとするなら, P(n6s | n_rolls, fake_die) は,式 P(n6s | n_rolls, fake_die) = Binomial (n_rolls, if (fake_die, 1/5, 1/6))を用いてとてもエレガントに指定できる.
 |
|
図 2: イカサマ・サイコロ問題のためのベイジアンネットワーク |
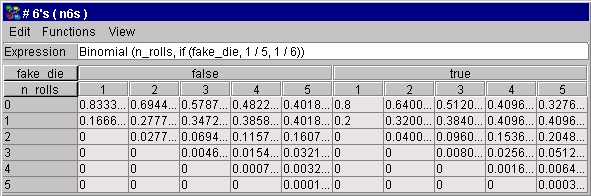
この式を指定するために,我々は 人々の数 の事例のように進めることもできるし,数式ビルダー("関数"メニューの"数式"サブ・メニューの"数式を作成"項目を選択して起動)を使用することもできる.指定の結果と生成された確率を図3に示す.
 |
|
図 3: 簡単な数式でとてもコンパクトに指定されたイカサマ・サイコロ問題のCPT |
同等に P(n6s | n_rolls, fake_die) = if (fake_die, Binomial (n_rolls, 1/5), Binomial(n_rolls, 1/6))を指定できることに注意.
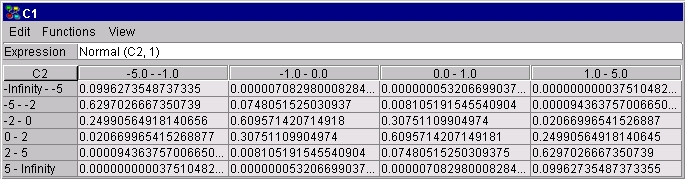
P(C1 | C2) が,C2によって与えられる平均と分散 1 を持つ正規分布で近似できると仮定する.ここでC2 は, ステート [-5,-1), [-1,0), [0,1), [1,5) を持つ区間変数である. 区間 [-infinity,-5), [-5,-2), [-2,0), [0,2), [2,5), [5,infinity)で与えられるC1 の離散化が適当であることがわかっているなら,我々は P(C1 | C2) を簡単に Normal(C2, 1) として指定することができる.図4参照.
 |
|
図 4: (区間)親変数 C2 で与えられる平均と分散 1 を持つ正規分布の離散化によって指定された変数 C1 のCPT. |
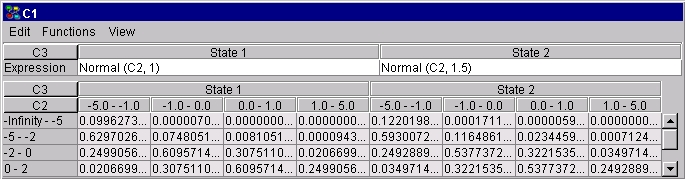
さらに,もしC1 が,"State 1" と"State 2"というステートを持つC3というラベルつきノードをもう1つの親ノードとして持っていて,その正規分布の分散が1で,C3 がステート "State 1" と 1.5にあるとき, C3 がステート"State 2"にあるとき,我々は,C3のさまざまなステートごとのさまざまな数式を指定できるいわゆるモデル・ノードとしてC3を定義できる.図5参照.
 |
|
図 5: C1 が,さまざまなステートのさまざまな数式の指定ができるモデル・ノードとして定義された新しい親ノードC3を得たことを除いては, 図 4 と同様. |
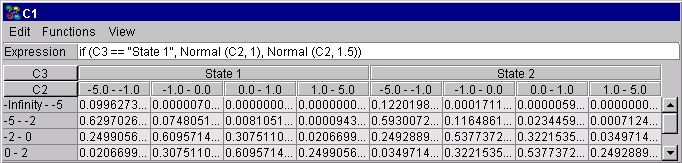
我々は,(モデル)ノードのステートで代替的に条件づけできるので,モデル・ノードの使用は厳密には必要ないことに注意せよ.しかしながら,モデル・ノードの使用は, しばしば,雑然とした指定を整然とさせ,読みやすく,メンテナンスしやすくする.たとえば,C3をモデル・ノードとして指定しない場合,P(C1 | C2, C3)は, 式 P(C1 | C2, C3) = if (C3 == "State 1", Normal (C2, 1), Normal (C2, 1.5))で指定できる.図6参照.
 |
|
図 6: C3をモデル・ノードとして指定する代わりに,2つの式が C3のステートで条件づけする1つの式に融合されてることを除いて,図 5 と同様. |
式を構成するために利用できる演算子と関数は,下記のとおり.
下記のバイナリ(2項)演算子が,数式に適用できる.
事例:
ここで C1 と C2 数値ノードの(すなわち,数字つきノードや区間ノード).
単項演算子を用いて数式を打ち消すことができる:
下記のバイナリ(2項)演算子が,ラベル(すなわち,文字列),数字,論理を比較するために使用できる(両方の演算対象は同じ種類でなければならない).等価演算子(すなわち,= と !=)だけは,ラベルと論理の式に適用できる.各演算子は,ブール値を返す.
事例:
ここで,C1 と C2 は,数値ノードである(すなわち,数字つきノードや区間ノード).
以下の関数は,数式の一覧の最小値と最大値を計算する.
事例:
ここで, C1, ..., C4 は,数値ノード(すなわち,数字つきノードや区間ノード).
以下の一覧は,単一の数式に適用できる標準的数学関数である.
事例:
ここで,C1 は,数値ノード(すなわち,数字つきノードや区間ノード).
床関数と天井関数は,実数表記の結果を整数に四捨五入する.
事例:
ここで C1 とC2 は,数値ノード(すなわち,数字つきノードや区間ノード).
modulo 関数は,2つの数値表記の割り算の余りを返す.もちろん,除数表記はゼロであってはならない.
事例:
ここで,C1 と C2 は,数値ノード(すなわち,数字つきノードや区間ノード).
条件式(3つの引数による)が指定できる:
事例:
ここで,FakeDie は論理ノードで,n は数値ノード,そして C1 と C2 は任意の(ただし同一の)タイプのノードである.
以下の標準的論理演算子が利用可能である.これらはすべて論理式を引数としてとる.
'and' の引数式の計算は,シーケンシャルに行われ,ある引数が 'false' と計算されると,計算を終了する. 同様に,'or' の引数式の計算は,ある引数が 'true' と計算されると終了する.
事例:
ここで, C1, C2, C3 は論理ノード.
たくさんの統計的連続分布が利用可能である.詳細は,連続分布を参照.
たくさんの統計的離散分布が利用可能である.詳細は,離散分布を参照.
| 関数 | ノードの条件 | 説明 | 引数 | 引数範囲 |
| Normal | 区間: 最初のステートは -infから始まる. 最後の区間は,Last infで終わる. | Mean | (-inf, inf) | |
| Variance | (0, inf) | |||
| LogNormal | 区間. | Mean | (-inf, inf) | |
| Variance | (0, inf) | |||
| Location (optional) | ||||
| Beta | 区間.最初のステートは下限で始まる.最後の区間は上限で終わる(引数参照). | 指定をしない場合は,引数の下限と上限は,それぞれ, 0 と 1 になる. | Alpha | (0, inf) |
| Beta | (0, inf) | |||
| Lower (optional) | (-inf, Upper) | |||
| Upper (optional) | (Lower, inf) | |||
| Gamma | 区間: 最初のステートは0の下で始まる.最後の区間は, infで終わる. | Shape | (0, inf) | |
| Scale | (0, inf) | |||
| Location (optional) | ||||
| Exponential | 区間: 最初のステートは0の下で始まる.最後の区間は, infで終わる. | Lambda | (0, inf) | |
| Location (optional) | ||||
| Weibull | 区間: 最初のステートは0の下で始まる.最後の区間は, infで終わる. | Shape | (0, inf) | |
| Scale | (0, inf) | |||
| Location (optional) | ||||
| Uniform | 区間: ステートの区間は,下限と上限をカバーする. - 少なくとも終点では(引数参照). | Lower | (-inf, Upper) | |
| Upper | (Lower, inf) | |||
| Triangular | 区間. | Min | (-inf, Mode) | |
| Mode | (Min, Max) | |||
| Max | (Mode, inf) | |||
| PERT | 区間. |
3-パラメータ型を用いる場合, Shape パラメータは 4. |
Min | (-inf, mode) |
| Mode | (min, max) | |||
| Max | (mode, inf) | |||
| Shape (optional) |
事例:
切り詰め演算子:
さらに,切り詰め分布を形成するために,切り詰め演算子を統計的連続分布に適用することができる.この演算子は,2つまたは3つの引数をとる.3つの引数が指定される場合,第1と第3の引数は,それぞれ左と右の切り詰め点を意味する数式で,一方,第2の引数は切り詰められるべき分布を意味する.
第1か第3の引数のどちらかは省略することができる.第1の引数を省略すると,右側切り詰め分布となり,第3の引数を省略すると,左側切り詰め分布となる.
事例:
| 関数 | ノードの条件 | 説明 | 引数 | 引数範囲 |
| Binomial | 数字つき: 0, 1, 2, ... , n | n | 0, 1, 2, ... | |
| p | [0, 1] | |||
| Poisson | 数字つき: 0, 1, 2, ... , n | n が確率を得る.n, n+1, ... の塊 | Mean | (0, inf) |
| Negative Binomial | 数字つき: 0, 1, 2, ... , n | n が確率を得る.n, n+1, ... の塊 | r | (0, inf) |
| p | [0, 1] | |||
| Geometric | 数字つき: 0, 1, 2, ... , n | n が確率を得る.n, n+1, ... の塊 | p | [0, 1] |
| Distribution | ラベルつき,論理,数字つき | 任意の分布を指定可能 | An arbitrary number of expressions | |
| Noisy OR | 論理 | ノン・ゼロ漏えい確率の指定が可能 | Parents | Boolean nodes |
| Inhibitors | [0, 1] |
事例:
<Expression> ::= <Simple expression> <Comparison> <Simple expression> |
<Simple expression>
<Simple expression> ::= <Simple expression> <Plus or minus> <Term> |
<Plus or minus> <Term> |
<Term>
<Term> ::= <Term> <Times or divide> <Exp factor> |
<Exp factor>
<Exp factor> ::= <Factor> ^ <Exp factor> |
<Factor>
<Factor> ::= <Unsigned number> |
<Node name> |
<String> |
false |
true |
(<Expression>) |
<Operator> (<Expression sequence>)
<Expression sequence> ::= <Empty> | <Expression> [, <Expression>]*
<Comparison> ::= == | = | != | <> | < | <= | > | >=
<Plus or minus> ::= + | -
<Times or divide> ::= * | /
<Operator> ::= truncate | Normal | LogNormal | Beta | Gamma | Exponential | Weibull | Uniform | Triangular | PERT
Binomial | Poisson | NegativeBinomial | Geometric | Distribution |
NoisyOR | min | max | log | log2 | log10 | exp |
sin | cos | tan | sinh | cosh | tanh |
sqrt | abs | floor | ceil | mod |
if | and | or | not
翻訳者:多田くにひろ(マインドウェア総研)