データの矛盾分析

矛盾分析は、変数値のオブザベーション（すなわち、エビデンスまたはデータ）間の可能な矛盾を検出し、追跡し、説明する動作です。オブザベーション間の矛盾が簡単に検出 (P(evidence) = 0)できますが、問題のある結果(fidings)も検出・追跡されるべきです。たとえば、診断のシチュエーションでは、単一の問題のあるテスト結果が、調査を完全に間違った方向に導くかもしれません。

データの矛盾は、メイン・ウィンドウのステータス・バーの右側とジャンクション・ツリー・ウィンドウ内に示されます （図１と図2を参照）。正の矛盾測度は、負に相関するオブザベーション（すなわち、正の矛盾）を示し、負の矛盾測度は正に相関するオブザベーションを示すことに注意してください。

図 1: 入力されたエビデンスについて計算された矛盾測度が、メイン・ウィンドウのステータス・バーの右側部に表示される。

 

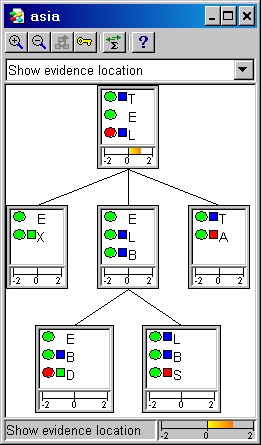
図 2: 入力されたエビデンスについて計算された全体的な矛盾測度は、ジャンクション・ツリーのルート・クリークとジャンクション・ツリー・ウィンドウのステータス・バーの右側部に表示されるに示される。サブ・ツリー中に入力されたエビデンスに関すｔるローカルな矛盾は、サブ・ツリーのルート・クリーク中に示される。

矛盾分析が何であるか、どのように使えるかを理解するには、下記の記事があります。

データ矛盾の定義

2つのオブザベーションの集合e1 と e2が負に相関しているなら、矛盾の可能性があると定義します。

正に相関する結果（findings）については、 P(e1|e2) > P(e1) で、逆もまた真なり、であると予想します（すなわち、 e2 を観測する e1も観測する可能性が高い（そして、逆ももまた真なり））。言い換えると、次のことが予想されます。

e1 と e2 が正に相関する場合、

P(e1,e2) > P(e1)P(e2)

e1 と e2 が負に相関しする場合、

P(e1,e2) < P(e1)P(e2)

e1 と e2 が独立の場合、

P(e1,e2) = P(e1)P(e2)

矛盾測度

したがって、オブザベーション（エビデンス）の集合 e = {e1,...,en}を仮定して、次のようの矛盾測度を定義します。



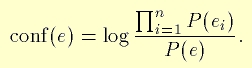
conf(e) が正の場合、e1,...,en は負に相関し、これらのエビデンスの間で正の矛盾を示します。（log関数の底の選択は重要ではありません。）

conf(e) が負の場合（すなわち e1,...,enの間に矛盾がなさそうな場合）、e1,...,en のすべてが正に相関しているという保証はないことに注意してください。これはローカルな矛盾が存在するときによく起こります（すなわち、conf(e) < 0　であるが、e　のある部分集合 e' については、conf(e') > 0 ）。f

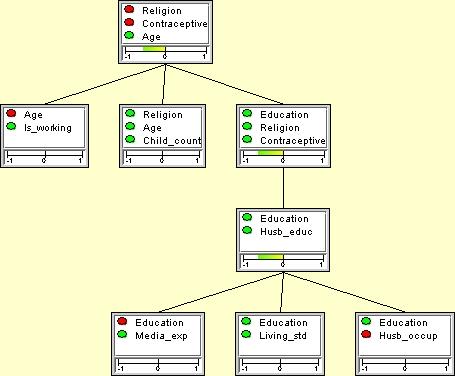
事例として、図3のジャンクション・ツリーを考えます。5個のエビデンス（赤いノードでマーク）があります。全体の矛盾測度は -0.54で、矛盾が示されていません。この測度は、ルート・クリークから得られています。

 

図 3: 入力された5個のエビデンス（赤いノードでマーク）に関する全体的な矛盾測度は、-0.54で、矛盾がないことが示されている。Education と Husb_occup ("Husband Occupation")の2個のエビデンスに関するローカルな矛盾は、全体の矛盾よりも小さいことに注意。

各クリーク中に示されている測度は、サブ・ツリー中の入力されたエビデンスに関するルートのクリークとの矛盾測度です。たとえば、ノード "Education" と "Husb_educ" を含むクリークの矛盾測度は-0.6で、 "Education" と "Husb_occup"に関連する2個のエビデンスに関係しています。.

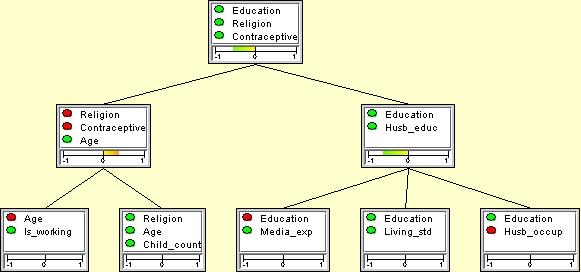
"Age"と "Religion"、"Contraceptive"に関連する3個のエビデンスに関するローカルな矛盾測度を計算するには、 たとえば、 クリーク { "Education", "Religion", "Contraceptive" } をルートとして選びます。（図４参照）（ジャンクション・ツリーのルート選択の詳細は、 ジャンクション・ツリー の章を参照）。 そして、3個のエビデンスの間にわずかな矛盾があることがわかります（矛盾測度は、0.39）。

 

図 4: 全体では矛盾がないが、"Age"と "Religion"、 "Contraceptive"の3つの変数について観測された値の間では、わずかな矛盾が存在する（矛盾測度は 0.39）。

矛盾の解決

実際には矛盾がないのに、正の矛盾測度が計算される場合があります。たとえば、次のような場合です。

記号のボタンを起動して、現在の矛盾を除去できるまだインスタンス化されていない変数のインスタンス化の可能性のリストを得ることができます。このボタンが起動されたときに現れるダイアログ･ボックスの例を図5に示します。

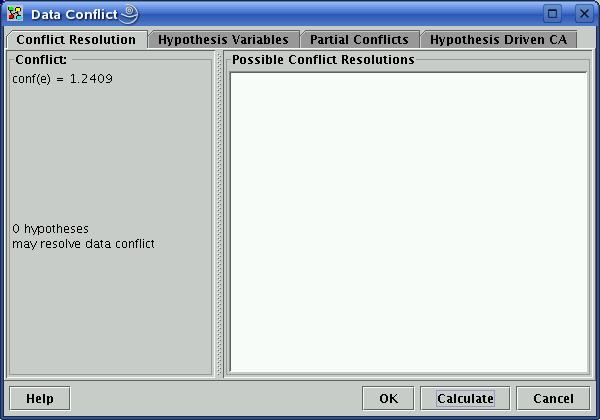
図 5: 矛盾解決ダイアログ・ボックス。このボックスは、現在の矛盾を除去できるまだインスタンス化されていない変数のインスタンス化可能性リストを含む。

ダイアログ・ボックスは、次の形式でインスタンス化可能性のリストを含みます。

<CM>:<variable>=<value>

ここで、 <CM> は、 <variable> が <value>　にインスタンス化された場合に得られる新しい矛盾測度です。0以下の結果の矛盾測度を持つインスタンス化のみが（もし存在すれば）表示されます。

インスタンス化ボタンは、現在選択されているインスタンス化（もしあれば）をエビデンスとして入力します。

矛盾の追跡

レアケースとして説明できない正の矛盾が観察されたときはいつでも、矛盾にあるエビデンスのピースをエビデンスのピースの多数意見でピンポイントすることが重要です。

基本的に、エビデンスの部分集合についての矛盾測度の計算を含みます。上に言及し説明されたように、ジャンクション・ツリー が、この目的のために役立ちます。例として、図6のジャンクション・ツリーを考えます。ここで、エビデンスのピースが４つ入力されています（赤いノードでマーク）。

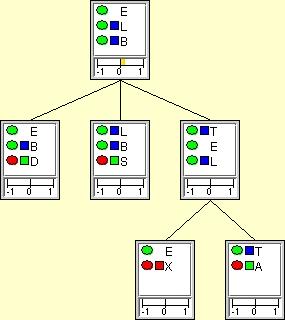
図 6: 入力された（赤いノード）エビデンスのピース間のわずかな矛盾。

0.21 の矛盾測度は、これらのエビデンスのピース間にわずかな矛盾があることを示します。矛盾の元を追跡するために、ローカルな矛盾測度を調査することができます。 上記のジャンクション・ツリーは、どのピースが矛盾の原因であるかの明確なカギをまったく明らかにはしていません。しかしながら、 クリーク{ T, E, L }から分かれるサブ・ツリーのローカルな矛盾測度はゼロで、ＸとＡのオブザベーションは、お互いに矛盾していないことを示します。

さらに調査するために、他のクリークをジャンクション・ツリーのルートとして選択できます。 If we select クリーク { T, E, L } をツリーのルートとして選択した場合（図7を参照）、Ｄの観測値とＳの観測値の間にわずかにローカルな矛盾があることがわかります。

図 7: D と Sの観測値の間のわずかなローカル・コンフリクト（矛盾）
Back

翻訳者：多田くにひろ（マインドウェア総研）