
適応アルゴリズムは, 逐次パラメータ更新に適しており,一方,EMアルゴリズム は,バッチ方式のパラメータ推定(すなわち,ケースの集合から条件付き確率のパラメータを推定)に適しています.
経験表は, 条件付き確率分布のパラメータでの事前経験を指定するのに使用します.適応は経験表を持たないノードとゼロの経験カウントを持つ親コンフィグレーションには無効であることに注意してください.
適応の使用を説明するために 経験表 の事例を使用します.図1にベイジアンネットワークを示します.このネットワークのドメインに関する詳細は, 胸部クリニック を参照してください.

図 1: "胸部クリニック"のベイジアンネットワーク表現.
あらゆる適応に先行する変数Smokerの(条件付き確率表(CPT)で表現された)条件付き確率分布は, (0.5,0.5)です.我々は,事例中のSmokerの経験カウントが10に設定されたと仮定します.ここで,ネットワークをコンパイルし,変数Sがステート0 ("yes")にあるオブザベーション(エビデンス)を入力し,適応ボタンここで,ネットワークを再初期化すると,変数 S のCPTが(0.5,0.5)から (0.667,0.333)に変わったことがわかるでしょう.また,Sの独立でないすべての変数は,異なる確率分布を持ちます.一般的に,観察された変数の先祖の変数の経験表が存在し,そのカウントがゼロより大きいならば,適応ボタンをクリックすると,それらのCPTが更新されます.経験表を削除または再設定することは,変数のCPTには影響しないことに注意してください.
値がなぜ変更されたかを理解するには,経験表をもう一度見るのが簡単です.編集モードに行って,変数"Smoker?" の経験表を見ると,初期カウント10に対応する現在の経験カウントが15で,その変数の5オブザベーションがなされたことがわかります.適応を開始する前の経験カウントは10で,確率分布は(0.5,0.5) ,すなわち,それらの5カウントが "yes"で,他の 5カウントが"no"でした..
追加の 5 カウントはずべてステート "yes"に属します.したがって,"Smoker?" の適応された確率分布は次式になります.P(Smoker="yes") = N("yes")/(N("yes")+N("no"))
= 10/15
= 0.667,
ここで,N("x") は,我々がステート "x"を経験した回数を意味します.その結果は,我々が見た値と一致します.下記は,ここまで我々が行ってきたことを簡潔に説明する適応の定義です.
要約すると,適応ステップは,エビデンスの入力,伝播(プロパゲーション),条件付き確率表と経験表の更新(適応)からなります.
下記で指定する実験を行うために,オリジナルなファイルで開始できるように,ネットワーク・ファイルを閉じて,Hugin グラフィカル・ユーザー・インタフェースがファイルを保存する用意を示している場合は "No" を選択してください.
図1のネットワークでは, "Tuberculosis or cancer"を除くドメイン内のすべての変数に経験表を追加するのが理にかなっています.それは,この変数が, logical OR であり,logical OR 変数上では経験表が得られないからです.すべての変数に経験表を追加("すべての離散確率ノードに経験表を追加"を選ぶ)してから,経験カウントを修正しなければなりません.なぜなら,それらは最初すべてゼロだからです.我々のケースでは,我々はネットワーク内の(変数"Tuberculosis or cancer"を除く )すべての変数に経験表を追加し,初期経験カウントを10に設定します.ネットワークは,これで適応の準備ができました.
前に述べたように,変数の経験表は,親コンフィギュレーションの経験カウントを表します.図 3 は,"Has Bronchitis"のCPTと経験表を示します.
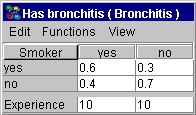 |
| 図 3: 適応前の "Has Bronchitis" のCPTと経験表 |
図3の解釈は,我々が20回"Has Bronchitis" の値を観察し,そのうち10回は, "Smoker?" がステート "yes" で,10 回は "Smoker?" がステート "no"であった,ということです.この情報と "Has Bronchitis"のCPTを組み合わせて,我々は,各個別のステートの初期経験に関する情報を得ることができます."Smoker?" がステート "yes" であるときに, "Has Bronchitis" が10オブザベーションあるので,
P(Has Bronchitis = "yes" | Smoker? = "yes") = 0.6,
そして
N(Has Bronchitis = "yes" | Smoker? = "yes") = 0.6 * 10 = 6,
ここで,我々は条件付き確率の表記法に則って, N の新しい表記を使用しました.同様に, Smoker?="no" については,N(Has Bronchitis="yes"| Smoker? ="no")= 0.3 * 10 = 3,
各ステートの合計経験カウントN("yes") = 6 + 3 = 9
および
N("No") = 20 - 9 = 11.
を与える.
これらの値で,今,ネットワークをコンパイルできて,何回か適応を実行できます.適応は,ネットワークを適応させるために,経験表も持つ変数が最低1つは必要です.経験カウントがセロでないか,すべての親コンフィギュレーションに同一の経験カウントを入力することが必要であることに注意してください. たとえば,初期経験カウントは,"10,0"に設定したかもしれません. 我々がこれまで行ってきた計算は,適応プロセスをより深く理解したいユーザーのみを意図しているので,あまり気にする必要はないことにも留意してください.
次のような5ケースを観察したとしましょう.
そして,このエビデンスを伝播します.次に,前にやったように,適応ボタンを5回クリックします.適応ボタンがクリックされるたびに,このオブザベーションの確率が増大します.ここで,前にやったように,ネットワークを再初期化して,"Smoker?" の条件付き確率分布を観察します.前と同様,我々が実行した適応は,変数"Smoker?"の文脈で行ったことと同じなので,その条件付き確率分布は (0.5,0.5) から (0.667,0.333) に変更されます."Has Bronchitis?"については,新しいCPT と更新された経験表が図4に示されます.
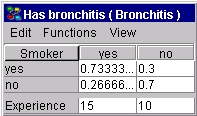 |
| 図 4: 適応後の"Has Bronchitis" に関するCPTと経験表. |
図 3 と 4 の右側(すなわち, P(Has Bronchitis = "yes" | Smoker? = "no") と P(Has Bronchitis = "no" | Smoker? = "no"))は変更されませんでした. これは,我々が実行した5回の適応は,"Smoker?" のステートが "no"のとき, "Has Bronchitis"のステートに関する新しい情報を何も与えずに,すべて変数 "Smoker?" がステート "yes"のエビデンスが入力されたからです.
一方,左側の列(すなわち P(Has Bronchitis = "yes" | Smoker? = "yes") と P(Has Bronchitis = "no" | Smoker? = "yes"))は,変更されて,いくつかの経験が得られたことを示しています.前の計算からの上記の結果を用いて,適応が実行され,我々は,N(Has Bronchitis = "yes" | Smoker? = "yes") = 6 + 5 = 11
N(Smoker? = "yes") = 15
P(Has Bronchitis = "yes" | Smoker? = "yes") = 11/15 = 0.7333
Hugin グラフィカル・ユーザー・インタフェースで表示される結果と一致する結果を得ました.これまでやってきた適応の手順は,最近の経験と古い経験に同じ重みを与えていました(つまり,あたかもオブザベーションが同時に行われたかのように,追加したり割ったりしただけです).しかしながら,しばしば,古いオブザベーションは,最近のオブザべーションよりも重要ではありません.したがって,我々は, それらのいくつかを非学習 または忘却しなければなりません.これは,新しいオブザべーション(エビデンス)が古いエビデンスよりも重要で,ゆえに適応プロセスにおいてより重みがかけられるべきだと言っていることと同じです.我々は,減退表を用いて,このような状況に Hugin を対応させることができます.
減退表は,経験表なしには意味がありません(すなわち,最初に覚えたことの何かを忘れるため).減退を実装するために,我々は以前のオブザべーションが忘却される比率である減退係数を導入しました. 0 の減退係数は適応がないことを意味し,1 の減退係数は減退がないことを意味します.
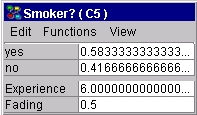
以下は,Hugin グラフィカル・ユーザー・インタフェースで減退表がどのように使用され,どのように働くかの説明です.これまで作業していたネットワークを保存しないで閉じるか,経験カウントを10に修正し,条件付き確率を(0.5,0.5)に戻します.変数に減退表を追加するために必要なステップは,変数に経験表を追加するのと同様です.離散確率変数に減退表を追加するには,変数を選択して,右クリックして, "経験/減退表の操作"サブメニューの"減退表を追加"を選択します.そして,ノード"Smoker?"についてのノード表の表示メニューの"減退表を表示"項目を選び, ノード表の減退表セクションで減退係数を入力します.減退係数は, 0 から1の間の数時であるべきです. 0 または1より大きい数字を入力した場合,何回ネットワークを適応させようとしても,何も変化がありません. 1を選んだ場合,減退が行われないかのように動作します.変数が経験表を持たない場合,その変数に減退表を追加することは不可能なことに注意してください.この事例では, 変数"Smoker?"に0.5の減退係数を入力します.ここで, Smoker? がステート 0 ("yes")にあるエビデンスを入力します.適応ボタンを1回クリックして,"Smoker?"の更新されたCPTと経験表を見るために編集モードに切り替えます.その結果を図5に示します.
 |
|
図 5: 適応後の "Smoker?"のCPT,経験表,減退表. |
気づくであろう1つのことは,経験カウントが10 から 6に減っていることです.ネットワークにいくつかの経験を追加しているのに,どうして経験カウントが減るのか?それを説明するために,減退係数について考えましょう.1回の適応が実行されたあと,確率は次のように計算されます.
N(Smoker? = "yes") = factor * N(previous_yes) + 1 = 0.5 * 5 + 1 = 3.5
N(Smoker? ="no") = factor * N(previous_no) = 0.5 * 5 = 2.5
N(experience) = 3.5 + 2.5 = 6
P(Smoker? = "yes") = 3.5 / 6 = 0.583333
P(Smoker? = "no") = 2.5 / 6 = 0.416667,
ここで,我々は再びいくらか情報 N の表記を用います. N(previous_yes) と N(previous_no) は,それぞれ,ステート"yes" と "no" にある以前の経験カウントで, N(experience) は,問題の変数の合計の経験カントです.ネットワーク中のすべての離散確率変数に減退表を追加するには, ネットワーク・パネルのどこかで右クリックして,"経験/減退表の操作"サブ・メニューの"すべての離散確率ノードに減退表を追加"を選択し,各変数の減退係数を追加します.翻訳者:多田くにひろ(マインドウェア総研)