ベイジアンネットワーク内の変数の確率分布の多く（またはすべて）が未知で，データ（すなわち，実験を実施して，または文献から，またはその他のソースから得られたオブザベーションの系列）からそれらの確率（パラメータ）を学習したいということがよくあります． EM (Estimation-Maximization) アルゴリズムとして知られるアルゴリズムは，とくにこのようなパラメトリック学習に有用で，これはデータかの学習のためにand it is the algorithm used by Huginで使用されているアルゴリズムです．EM は，観察された（しかし，しばしば完全ではない）データからネットワークのモデル・パラメータ（確率分布）を発見しようとします．
EMアルゴリズムは，バッチ方式でのパラメータ推定（すなわち，条件付き確率表のパラメータの推定）によく適しており，一方，適応アルゴリズム は，逐次型のパラメータ更新によく適しています．経験表 は，条件付き確率分布のパラメータでの事前経験を指定するために使用されます． EMパラメータ推定は，経験表のないノードには無効であることに注意してください．
EM学習の使用を説明するために，経験表 の事例を使用します．このベイジアンネットワークは図１に示します．
このネットワークのドメインに関する詳細は，胸部クリニックを参照してください．
図1: "胸部クリニック"を表現するベイジアンネットワーク.
EM 学習の使用を説明するために，ネットワークの構造が図１に示すようにわかっていることを仮定します．さらに， "Has tuberculosis" と "Has lung cancer" を仮定した"Tuberculosis or cancer"の条件付き確率分布が 分離である（すなわち，その親の1つがステートyesである場合のみ，子がステートyesにある）ことが知られていると仮定します．
我々は，残りの分布の集合での，どのような事前知識も仮定しません．したがって，我々は，ノード"Tuberculosis or cancer" を除いたすべての条件付き確率分布の入力を1に設定します．これは，ノード"Tuberculosis or cancer" 以外のすべてのノードの確率分布を一様分布に変えます．なぜなら，Huginは，列の値の合計が1でない場合，その分布表の値を正規化するからです．一様分布は，無知（すなわち，ある変数の確率分布についての事前知識が何もないこと）を意味します．図２は，パラメータ推定に先行する初期周辺確率分布を示します．
図 2: 条件付き確率表ですべての値を1に設定したあとの確率分布.
さて，このネットワークに関連づけられたデータ・ファイルから確率を学習しましょう．編集モードで"EM-学習" 
ボタンを押します．ボタンを押すと，EM 学習ウィンドウが現われます．次に，"ファイルを選択" ボタンを押して，条件付き分布確率を学習するファイルを選びます．このネットワークと同じディレクトリに置かれている
asia.dat ファイルを選びます．このファイルの最初の数行を下図に示します．
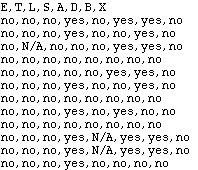
図 3: asia.dat ファイルの最初の数行
第1行目は，ネットワーク内のノードの名前で，残りが各実験／観察のエビデンスです．エビデンス "N/A" は，対応する変数での観察（オブザベーション）がなかったことを意味します． ファイルが選択されると，図4に示す "OK" ボタンが現れます．
図 4: EM-学習ウィンドウ
"OK" ボタンを押すと，EM-アルゴリズムがステートします．データに基づいて，EM-アルゴリズムが各ノードについての条件付き確率分布を計算します．図 5 は，EM-学習終了後の新しい条件付き確率分布を示します． 図５からわかるように，すべての条件付き確率分布の値が，ケース・ファイルのすべてのケースを反映して変更されています．
図 5: 推定された周辺確率分布.
図6は，ケースの集合が生成されたネットワークの周辺確率分布を示します．ここに示す確率分布は，オリジナルの胸部クリニック・ネットワークのものであることに注意してください．
図６: オリジナル・ネットワークの周辺確率分布
翻訳者：多田くにひろ（マインドウェア総研）