予測
SOMの古い研究では、クラス分類の場合と同様、学習されたノードの目的変数の値によって予測(回帰)を行う研究がありました。しかし、残念ながら、これはあまり賢いやり方ではありません。SOMのアルゴリズムが、説明変数と目的変数の関係をモデルしようとしていないという事実よりも、目的変数の値が連続値であるということが致命的です。そもそもSOMのノードは、データ空間内に離散的に配置されていますので、SOMだけでは離散的な要約にしかなりません。目的変数の値がカテゴリ値(離散値)の場合は問題になりませんが、連続値を離散値で予測するのでは原理的に予測誤差が小さくなりません。
しかし、SOMのノードが格子状につながっていて、多次元空間内で自由曲面を形成して、全体としてデータ分布の非線形な要約になっていることは捨てがたい特長です。どうしたらこれを予測モデルに利用できるのか?その答えは、SOM自体を予測モデルとして使用するのではなく、予測モデルの”足場”に利用するということです。ざっくりと単純化して言えば、ノードごとに伝統的な線形回帰モデルを作成すれば、従来の線形回帰の枠組みに則りながら、従来の線形回帰を非線形近似へと拡張できるということです。

SOMローカル回帰手法のコンセプト
学術的には、SOMのノードごとに人工ニューラルネットワークによる予測モデルを作成する方法も研究されておりますが、人工ニューラルネットワークは、単純に予測値を求めることには役立つのですが、モデルを解釈するには不向きです。すでにSOMによって全体的なおおよその非線形構造を要約できているのですから、ローカル(局所)・モデルは線形でよいわけです。
Viscovery Predictorが提供するSOMローカル回帰モデルは、SOMによる予測モデルではなく、正確に言うと、SOMを基盤としたローカルな線形重回帰モデルの集合です。まず伝統的な線形重回帰分析を行い、その残差を新たな目的変数(ターゲット値)として、ノードごとのローカル回帰モデルを作成します。したがって、ノードごとに各変数の回帰係数が 求められますが、それは全体の線形モデル(グローバル回帰)を基準にして、非線形モデルが必要なノード(部分空間)のみに現れます。グローバル回帰による予測値を非線形近似に修正するためのモデルが、SOMローカル回帰だというわけです。
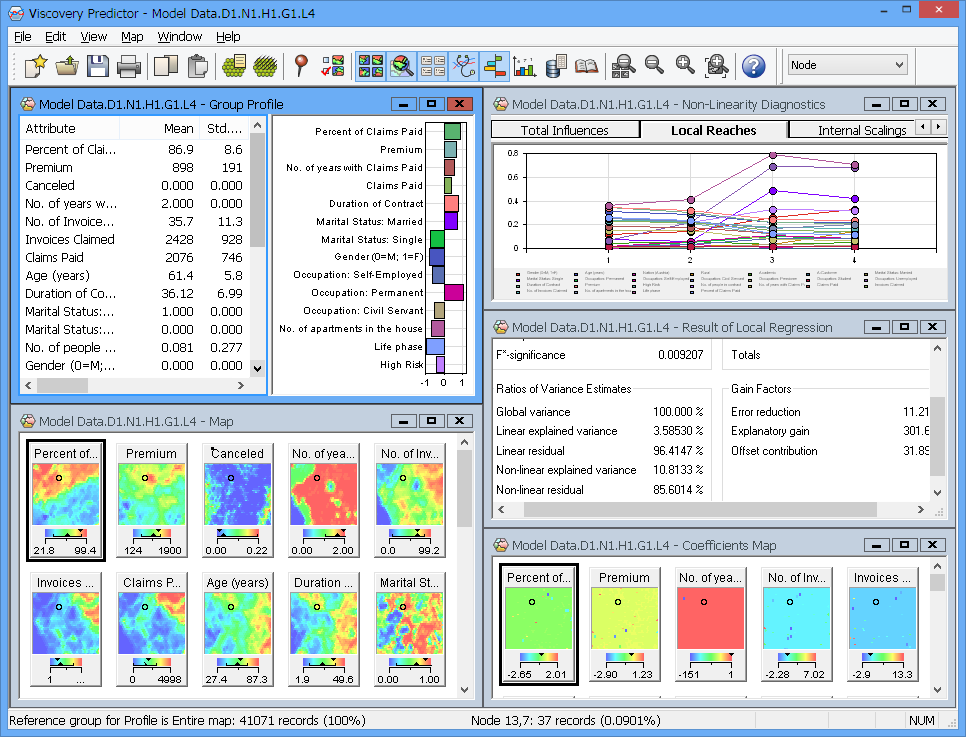
予測モデルの画面
たとえば、大型ビルやデータセンターなどの電力需要の予測では、季節や天候、曜日、時間帯などさまざな状況によって、異なる予測モデルを適用する必要があります。あるいは半導体製造プロセスの歩留まり予測では、環境の気温や湿度、各工程の製造装置のたくさんの設定値やセンサーからの測定値などにより、工程の状態がたくさんの数に分類されます。これらの応用では、単一の予測モデルですべてのケースに対応することはできません。現状、このような予測モデルを作成するのは、非常に複雑なプロセスであり、また、そうして作成したモデルをメンテナンスすることが非常に困難です。
国内では、大手電機メーカーが「大量データ中に混在する異なるパターンや規則性を自動発見する技術」をつい最近実用化したとして話題になっているのですが、どうやらその中身は樹形図モデル(決定木)で、大量データをさまざまな条件づけで分割して、データの部分集合ごとに予測モデルを作成することのようです。残念ながら、そうしたルールでデータを分割する場合、より精緻な分析のためには、よりたくさんのルールでデータをより細かく分割しなければなりませんが、ルールが増えれば増えるほど、ルールのメンテナンスが困難となり、また、その結果、データの部分集合が小さくなりすぎると、個々のモデルの信頼性を十分に維持するのが難しくなります。
SOMローカル回帰では、SOMのノードの数だけローカルな予測モデルを作成できますので、その数は1000個とか2000個となります。つまり、国内のメーカーが開発した技術よりも、もっとたくさんのローカル・モデルを作成して、より精度の高い予測が可能です。しかも、このようにたくさんのローカル・モデルを作成しても、個々のローカル・モデルの信頼性が維持できます。その秘密は、データを完全に分割してしまわずに、SOMによってデータ分布のトポロジーが維持されているので、周辺のデータレコードを重みづけしながら予測モデルの学習に利用できるからです。Viscoveryは国内メーカーよりも約10年早く、2003年には、より高度でスマートな技術を完成させております。
SOMローカル回帰モデルは、このようにさまざまな状況に対応する予測モデルを短期間で作成し、迅速にメンテナンスしていく場合に有効な手法です。
