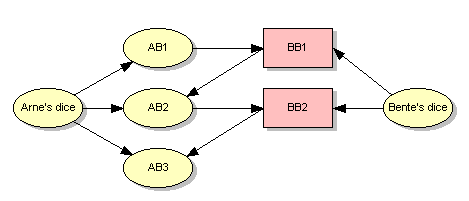
 |
| 図 1: インフルエンス・ダイアグラムでの確率変数と決定変数，およびそれらの従属性 |
このドキュメントは，"Taekeboks"というサイコロ・ゲームの単純なバージョンをモデルするために，インフルエンス・ダイアグラムをどのように構築するかを説明する．このモデリングの目的は，相手の推定される戦略に対抗する勝利戦略を発見することである．Huginでインフルエンス・ダイアグラムを設計して，その後で実装する．最終的に，こ実装は相手の推定される対抗する最適戦略を決定するために使用される．
このドキュメントは，Sren Andersen, Lisa Elgaard, Brian Jensen, Brian Kristiansen および Sren MogensenのサポートによってMichael Ho"hle が著したものである．ネットワークとそのドキュメンテーションは，1997年秋にAalborg 大学のコンピュータ・サイエンス学科でのグループ C1-213 によって実施されたDAT3（第7学期）プロジェクトに由来する．DAT3 プロジェクトの指導教官はDennis Nilssonだった．
下記のようなサイコロ・ゲームTaekeboksの簡単なバージョンを考える． Arne と Bente (典型的なデンマーク人の名前）という2人のプレーヤがゲームに参加する．各プレーヤ は（ "1" と "2"がラベルづけされた）2面のサイを持つ．
最初に両者はお互いに結果を見せないでそれぞれのサイを投げる．このゲームの目的は，自分のサイの知識に基づいて，どれだけ同一の値が出るかを推測することである． 以下のビッド（入札）が可能である:
Arneがゲームを開始するとする． 彼は上記の4つのビッドから１つを選ぶ．Arneのビッドに続いて，Benteは Arneのビッドを信じてビッドアップ（競り上げ）するか，コールする（提示を求める）かを決定しなければならない．もしBenteがコールしない場合，Arneが Benteの新しいビッドを考える番になる．このゲームは，一方のプレーヤがコールを決定するまで続く． コールは，両者が彼らの目を明かすことでなされ，したがって，どちらがコールアップしたビッドがテーブルの上にあるかないかを解決することである．このプロセスがゲームの勝者と敗者を決定する．
ある霧のかかった夜に上記のゲームを数ラウンドすることをあなたの親友Arneに説得することを想像してみよう．ことをより面白くするために，各ゲームの敗者は次のラウンドのビールをおごらなければならない． あなたがしこたま酔うほどArneにおごらせるには，あなたはどのように行動するべきか？言い換えると，Benteにとってのよい戦略は何か？
いくつかのアプローチがある．たとえば，ある人はゲーム理論の方法によって上記のゲームを分析するだろう，またある人はインフルエンス・ダイアグラムを用いようとするだろう．ゲーム理論はとても複雑で扱いにくい傾向があるので，我々は後者に集中しよう．
Arneの戦略を推定して，我々は最適な対抗戦略を発見するためにインフルエンス・ダイアグラムを解く．重要な問題は，いかにしてArneの戦略をよく推定するかである．我々はあなたがArneと簡単なTaekeboksのゲームをとてもたくさんプレイしてきており，彼の戦略をよく知りつくしているとしよう．
単純化するために，ここではArne が常にリードしていると仮定する．すなわち，彼は常にゲームでビッドの先手である．
最初に我々は必要な確率変数と決定変数がどれで，それらがどのようなステートを持つかを見つける必要がある．これを獲得する用心深い方法は，我々のゲームのアクターと彼らが実行するアクションを見つけることである．
| アクター: | Arne, Bente |
| 決定者: | Bente |
| アクション: | サイを投げてビッドする（コールを含む） |
1ゲーム中のビッドの最大のシーケンスを分析することにより，各プレーヤのビッドの最大量を決定する．
| Arne | Bente | Arne | Bente | Arne |
1 |
2 |
2・1 | 2・2 | コール |
Arneは，1ゲーム中に最大３回ビッドを持つ．Benteの最大は２回のビッドである．
各アクションは，ここで次のルールにより確率変数か決定変数のどちらかに変換される: アクションが決定の場合，決定者がするべきことは決定変数に変換され，それ以外は確率変数になる．その結果は：
| 確率変数 | Arneのサイ, Benteのサイ , Arneの1番目のビッド (AB1), Arneの2番目のビッド (AB2), Arneの3番目のビッド(AB3) |
| 決定変数 | Benteの1番目のビッド (BB1), Benteの2番目のビッド (AB2) |
サイを振った結果にはBenteが影響を持たないので，Benteのサイを振った彼女の結果に対応する変数 "Benteのサイ" は確率変数となることに留意せよ．
我々のインフルエンス・ダイアグラムの変数を明らかにすると，次にそれらが持つべきステートを考える．サイ変数のステートがサイを振った結果を表すのに対して，ビッド変数のステートはそのビッド変数の時点での可能なビッドを反映する．ステートの数が最大のビッド・シーケンスによることに留意せよ．
| 変数 | ステータス |
| Arneのサイ, Benteのサイ | 1,2 |
| AB1 | 1,2,2・1,2・2 |
| BB1 | 2,2・1,2・2,コールl |
| AB2 | 2・1,2・2,コール |
| BB2 | 2・2,コール |
| AB3 | コール |
次の作業は，見つかった変数間の従属性（依存性）を- リンクで表現して- 確立することである．我々のリンクの目的は次の２つである：
単純な Taekeboksのプレーの経験から，ビッドするときに通常自分自身のサイの目と相手の最新のビッドのみを考慮することがわかる．この２つの目的と上記の経験は，図１に示すダイアグラムになる．
| |
| 図 1: インフルエンス・ダイアグラムでの確率変数と決定変数，およびそれらの従属性 |
Arneの最初のビッドの戦略は，彼のサイの値にのみ従属することに注意せよ．我々は彼の戦略を正確にはわからないが，我々は最善の推量を用いる．
決定変数を導入すると，意思決定の結果を決定する効用関数を追加することも必要になる，我々の効用関数には２つのゴールがある．
すべての効用を持つ結果のダイアグラムを図２に示す． 項目 1 を確実にするため，効用関数は連続するビッドの間に置かれる（たとえば，U5 は BB1 と AB2の間）． これらの関数は，連続するビッド変数と２人のサイ変数の両方に接続される．後のビッドがコールであったかを確認するため，そしてコールの前のビッドが存在したかどうかを確認するために，これらのすべての情報が必要である．このステップは，効用関数U4,U5,U6,U7をもたらす． 項目 2 は，AB1 と BB1 (U1) の間，および AB2 と BB2 (U2)の間に効用関数を置くことによって達成される．後で効用関数に値を割り当てるとき，禁じられたアクションにはすべてとても低い値が割り当てられる．
 |
| 図 2: 我々のモデルのインフルエンス・ダイアグラム． U1 と U2 はBenteのビッドが有効で あることを保証し，U4, U5, U6, U7は Bente が勝つか負けるかを決定する． |
U1の親の集合はU4の親の部分集合であるので，この２つは加法的に組み合わせることができる．これは単にU4の適切な列中でU1の効用値がU4の値に加えられることを意味する．Similarly U2 と U6 は単純に組み合わさる．結果のインフルエンス・ダイアグラムを図３に示す．
 |
| 図 3:簡単なTaekeboksをモデルする最終のインフルエンス・ダイアグラム．効用関数がどのように組み合わせられたかに注意． |
変数，関数およびそれらの従属性を決定してから，確率変数に条件付き確率を，効用関数に効用値を割り当てる必要がある．この作業は3つのサブタスクに分割できる．Huginで実装された正確な表の詳細は， 重要なことではないが興味深いことを含む．
この作業を遂行するために，Arneの戦略をよく推量することが必要である．単純化のために，我々は彼がとても合理的な決定戦略に従うと仮定する：
実際のゲームでは，Arneは彼の本当の戦略を秘匿するために，非決定論的戦略に従うであろう．最適な対抗戦略をどのように見つけるかのコツを会得すると，非決定的戦略に対抗する戦略を速攻で見つけるためにもインフルエンス・ダイアグラムを用いることができる． [詳細]
Arneの戦略に対抗するBenteの最適な対抗戦略を見つけるためにインフルエンス・ダイアグラムを使用する準備ができた．
|
Huginでの下記のアルゴリズムが望ましい結果をもたらす：
ステップ 2.1 において，AB1の可能なステートでのみループする．Arneの戦略によって，たとえば，Arne がAB1でbids 2・1 をビッドすることは不可能． |
ゲームが続く限り，BB2での最適アクションを決定するために，BB1での最適アクションをエビデンスとして投入し，AB2でのステートでループすることが必要になる．しかし，Benteが本当に2回ビッドすることはないので， このステップはアルゴリズムに含まれない．
このアルゴリズムを適用することによって，以下のBenteの対抗戦略が決定される：
| Benteのサイ | |||
| 1 | 2 | ||
| Arneの1番目のビッド | 1 | 2・1 | 2 |
| 2 | 2・1,2・2,コール | 2・2 | |
| 2・1 | NA | NA | |
| 2・2 | NA | NA | |
たとえば，Benteが 2 を出し，Arneが最初のビッドで 2 をビッドすると，戦略はBenteに 2・2をビッドすることを教える. Benteが１を出し，Arneが２をビッドするシチュエーションでは，2・1,2・2 およびコールの３つのアクションが等しく良い．決定論的戦略を得るには，単に可能性の１つを選択するので十分である．表中のNAは，Arneの戦略の選択によって，そのシチュエーションが起き得ないことを表す． Benteの選択のすべては，したがって，等しく良い．
問題は，この対抗戦略が実際にどれぐらい良いかである．４つの可能なサイのコンフィギュレーション ([AD=1 and BD=1], [AD=1 and BD=2], [AD=2 and BD=1], [AD=2 and BD=2]) での２つの戦略の間でゲームをシミュレーションすることにより，Bente はwill win 75%のゲームに勝つことが明らかになる！言い換えると，12ラウンド中， Bente（あなた）はたった3回ビール代を払えばよいのに対して， Arneは 9回払わなければならない. 乾杯！
Taekeboksゲームの簡単なバージョンをモデルするインフルエンス・ダイアグラムが，Huginで設計され，また実装された，結果のダイアグラムが図３に示され，Huginの実装は， Hugin のWebサイトからダウンロードできる．
Arneの戦略が推測されて，ダイアグラムの表に投入された．エビデンスを投入し，プロパゲート（伝播）するためにHuginを用いて，ゲームの75%で勝つことのできるBenteの最適な対抗戦略を見つけることができた．
このゲームのゲーム理論的分析は，Arneについて仮定された戦略がとても良いものではないことを明らかにする．たとえば，彼は常に2・(彼が出した目)をビッドする戦略を好むかもしれない．Benteがインフルエンス・ダイアグラムで対抗戦略を見つけたとしても，これによって彼は確実にゲームの50％に勝てる！（ゲーム理論的注意：この戦略コンビネーションは，双方のプレーヤが引き分けになるナッシュ均衡を形成する．）
Arneが決定論的戦略をとるという仮定は，あまり現実的でない．Arneのビッド変数の表で値を変更することにより，Arneは簡単にプレイをランダム化戦略で修正できる．上記のアルゴリズムは，Arneのランダム化戦略に対する決定論的対抗戦略を見つけるためにも働く．
簡単なTaekeboks は，まったく退屈なゲームだ．楽しみを増加するための可能な拡張は： サイコロの面を増やしたり，プレーヤのサイコロを増やしたり，ジョーカーの概念を取り入れたり，さらにはプレーヤを増やしたりすることだろう．問題は，わずかな拡張でもインフルエンス・ダイアグラムが爆発的に複雑になることである．
コメントまたは質問は， hoehle@dina.kvl.dk にお寄せください．
このネットワークは，Huginソフトウェアとともにコンピュータにインストールされています．Huginグラフィカル・ユーザー・インタフェースでネットワークを開いてください．（注意：すべてのブラウザがHuginのディレクトリを開けるとは限りません）．Huginをインストールしたディレクトリ（たとえば， C:\Program Files\Hugin\Hugin Lite\Samples) にこのネットワークがあります．Hugin のダウンロード・エリアにもサンプルがあります．
翻訳者：多田くにひろ（マインドウェア総研）
